周向宇院士：中国古代数学的成就

发布时间：2024-01-25

「编者按」“中国古代数学的贡献”一文，作者系周向宇院士。在研究专业数学之余，作者将学习和研究中国古代数学的心得体会与研究成果整理成文，刊发于《数学学报，中文版》2022年第4期。该文阐释与揭示了中国古代数学对华夏文明的贡献，对国学、语言、文化的影响，以及对现代数学的影响与贡献。“数学大院”公众号将陆续以推文呈现，让读者从多方面领略中国古代数学的成就与贡献。

1706144325(1).png

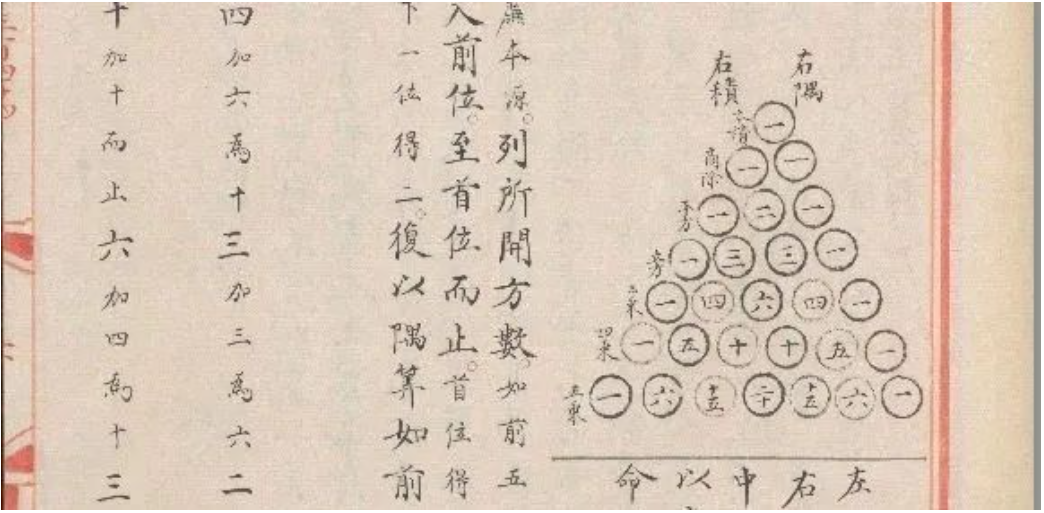
图片来源：永乐大典.卷16343-16344.算字.明嘉靖隆庆间内府重写本.剑桥大学图书馆藏

以下内容节选自“中国古代数学的贡献”一文第三章“中国古代数学的成就”，作者系周向宇院士。

3.1 代数思想

中国古代很早就有了零的思想，比如在筹算中用空位表示零。零不仅指各个数位上的零(用空位表示，后用圆圈O)，也包括运算结果中的零。中国古代很早就引进了负数，在《九章算术》里就很明确地引进了负数、加法的逆运算减法及其运算规则(交换律、结合律)，乘法的分配律，乘法的逆运算及分数及其运算律，这是数学发展中的一个里程碑。所以说，中国古代数学最早认识、发现、引进了第一个无限群、环、域(整数群、整数环、有理数域)；另外还引进了矩阵(matrix)，发现了消元法(Gaussian elimination)，解决了线性方程组求解问题(Cramer's Rule for system of linearequations)。

《九章算术》是一部十分重要的数学著作，总结了战国、秦、汉时期的数学成就，西汉的张苍、耿寿昌等曾经做过增补和整理，后来刘徽给它作了注解。虽然最后成书于东汉前期(公元一世纪左右)，但许多内容显然早已存在于先秦。这从刘徽为《九章算术》作的注就可看出。负元(逆元)、逆运算及其运算规律的引进使得运算变得方便灵活，完满解决了运算问题，为抽象代数的产生奠定了基础。对其意义与价值，套用拉普拉斯关于十进位值制的话来评价是不过分的。

3.2 天元术

中国古代数学用算筹计算圆周率，开平方根、立方根和更高次的根，对多项式方程进行数值求解。此外，中国古代数学还引进了未知量“天元”，国家自然科学基金有一个“数学天元基金”，就是为了纪念中国古代引进了变量、未知量、待定量。“宋元四杰”李冶、秦九韶、杨辉、朱世杰建立、整理和发展了天元术，而到了朱世杰时期已经发展成为了天、地、人、物四个变元。

在宋元四杰时期(大约为十三、十四世纪)，中国数学的发展达到了一个高峰，比如十进分数。比如秦九韶的大衍求一术(1247年)，这个结果被称为中国剩余定理(高斯后来重新发现)。又比如高次方程的数值解法，也是秦九韶基于很多古代数学家的贡献发展总结而来的。西方在19世纪重新发现这个方法，并称为霍纳方法(Horner's scheme)，在前苏联编撰的《数学百科全书》的相应条目“Horner's scheme”里、

3.3 极限思想

再来谈谈中国古代的极限思想。《庄子·天下》有句惠子名言: “一尺之棰，日取其半，万世不竭。”第一天取木棰长度的，第二天取，到了第天取，万世都不会穷尽。写成式子，即

1706145226(1).png

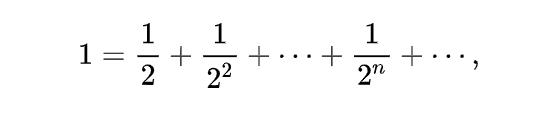
后面必然需要省略号“......”。

另外，《墨子·经下》有句话的意思是说，一条线段从中点分为两半，取其一半再破成两半，仍取一半继续分割，直到不可分割时就只剩一个点。《墨子·经下》：“非半弗[著斤] (编者注：该字左著右斤，读作zhuó，因GBK编码无法显示该生僻字，故本文以[著斤]代替)，则不动，说在端。”这里，[著斤](zhuó) (注：有的书也用斫)意指：用刀斧砍。《经说下》曰：“非[著斤]半，进前取也。前则中无为半，犹端也。前后取，则端中也。[著斤]必半，毋与非半，不可[著斤]也”。墨子的半分法体现了(事实上等价于)区间套原理。半分法可以用来证明数学分析里的几个重要、被认为有难度的定理。比如证明致密性定理、聚点定理、有限覆盖定理，还有连续函数的零点存在定理、Henstock--Kurzweil积分中的基础---Cousin引理(对闭区间上的任一正函数，总存在闭区间的-细度分划(-fine Perron partition)) (HK积分仅对黎曼积分做些许改动，就蕴含了勒贝格积分)，其实用的都是墨子的半分法。

另外，惠子的取半、墨子的半分及王尔的半中说明古人应该很早就会用尺规平分线段。

刘徽和祖冲之的“割圆术”也蕴含了极限的思想。祖率(密率)

是非常巧妙的。祖冲之和他的儿子祖暅编写了《缀术》，这本书是唐朝算学科最难的课本。祖暅原理“幂势既同，则积不容异”，就是说：如果两个立方体的所有等高的横截面积全都相等，则它们的体积必相同(这里“既”是“全、都”之意)。这在微积分里被西方称为卡瓦列里(Cavalieri)原理。祖暅用其原理求出“牟合方盖”的体积，进而得出球体积，解决了刘徽遗留问题。

《缀术》代表了当时数学的最高水平，但“学官莫能究其深奥，是故废而不理”，这本书最终失传了，这是十分遗憾的事情。在我看来，《缀术》蕴含极限思想，光从书名来看， “缀”就有连续的含义。

明朝数学家王文素及其《算学宝鉴》对数学有重要贡献，比如对于17世纪微积分创立时期出现的导数，王文素在16 世纪已发现并使用。

上述成就当然是基础数学的成就，只是中国古代数学的一小部分。

参考文献

[1] 毛泽东, 改造我们的学习, 毛泽东选集第三卷, 北京: 人民出版社, 1991:797.

[2] Cajori F., A History of Mathematical Notations, Dover Publications, Inc. New York, 1993:70.

[3] Gowers T. (Ed.), The Princeton Companion to Mathematics, Princeton University Press, 2008.

[4] 吴文俊, 对中国传统数学的再认识, 百科知识, 1980年第7--8期.

[5] 程贞一, 闻人军, 周髀算经译注, 上海: 上海古籍出版社, 2012.

[6] 卡尔·博耶(Carl B. Boyer)著, 尤塔·梅兹巴赫(Uta C. Merzbach)修订, 数学史(修订版), 中央编译出版社, 2012.

[7] 吴文俊主编, 世界著名数学家传记, 花拉子米, 北京: 科学出版社, 1995.

[8] 李文林, 数学史概览, 北京: 高等教育出版社, 2000.